THE 3rd STATE OF MATTER – What is a Real Gas?

In any scientific discipline when we want to  learn and understand the basic principle about how things work, we need a reference model defined in clear and simple terms so that it can be easily used and applied. When we deal with gases, the theoretical model of reference is called Ideal Gas. The Ideal Gas also called The Perfect Gas, is a theoretical case in which the behavior of gases is described by the relation between the main characteristics of gases expressed in an equation know as the Ideal Gas Law . This is:

PV = nRT

Where:

• P = the gas pressure;
• V= the gas volume;
• n = the number of moles of the gas;
• R = the universal perfect gas constant;
• T = gas temperature.

What the Ideal Gas law says is in fact how much energy is needed in order to make a gas effective for a certain application. In the International System of Units, energy is measures in joules (J), volume is usually in cubic meters (m³), force is in Newton (N), Temperature in Kelvin degrees (K) and pressure in pascals (Pa) (where 1Pa = 1N/m²). A force of 1N moving through a distance of 1m does 1J of work. Thus, both the products PV and nRT have the dimensions of work (energy).

This Ideal gas law obeys the Kinetic Molecular Theory stated on 5 postulates as follows:

• POSTULATE 1 => gas consist of particles in constant motion and which collide elastically between one another and the container;
• POSTULATE 2 => gases are mostly empty space, the occupied volume is negligible;
• POSTULATE 3 => gas particles exert pressure when colliding with the container;
• POSTULATE 4 => gas particles don’t interact with each other, there are no intermomecular forces involved;
• POSTULATE 5 =>  average molecular speed of gas particles (their kinetic energy) is proportional to temperature.

THE REAL GAS LAW

Real gas, in contrast, has real volume and the collision of the particles is not elastic, because there are attractive intermolecular forces between particles. As a result, the occupied volume of real gas is much larger than of the ideal gas, and the pressure of real gas is lower than of ideal gas. To make the distinction between real and ideal gases the compressibility factor (Z) was introduced. This tells us how much the real gases differ from ideal gas behavior and has the following mathematical expression:

Z = PVnRT 

• Z = 1 for ideal gases;
• Z ≠ 1 for real gases

NOTE: For of Avogadro Nr.  (N_A = 6.02214076×10²³ mol^-1 ) we are not restricted to these conditions. For example, we could change the volume for these gases to be higher or lower and change the pressure and temperature to be equally higher or lower as well. As long as all three conditions are the same for all gases, we can then say that they all have the same number of molecules! The number may not be Avogadro’s number any more, but the number of molecules can still be calculated.

From this new observations, In 1873, the Dutch physicist Johannes Diderik van der Waals came up with a modification of the ideal gas law, describing the deviation of real gases from the ideal gas. He introduced 2 new correction factors one for Pressure and one for Volume. The final form of van der Waals equation for real gases is expressed as follows:

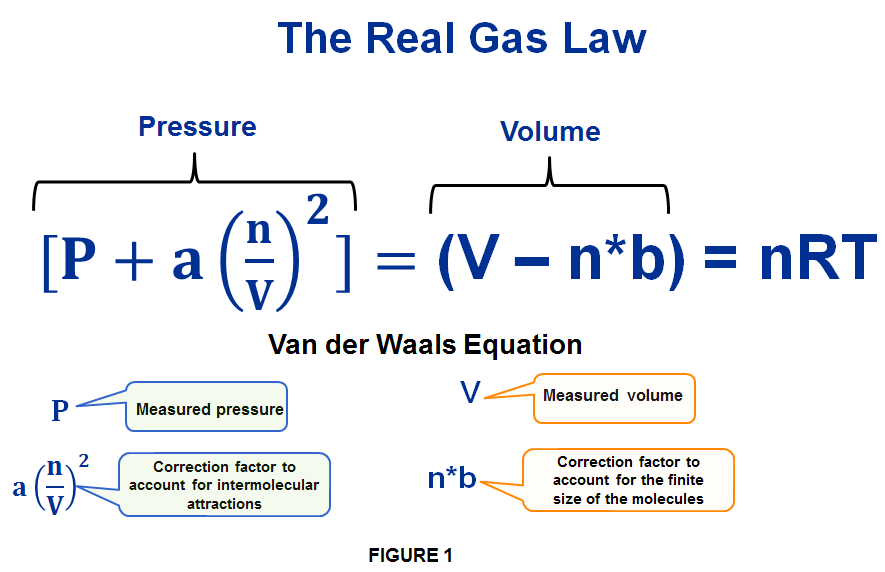
As you can see the right hand side of this equation for real gases is exactly the same like for ideal gases (nRT). So let’s focus on the left-hand side and understand what exactly J.D. van der Waals meant.

First let’s look at PRESSURE term as introduced by van der Waals for real gases. In this equation P is the measured force. Yet as mentioned earlier, the kinetic molecular theory assumes that there are no intermolecular forces between gas particles. But in real gases there are such attractive forces and these hold the gas molecules back a bit. The is because the pressure in real gases is actually lower than of the ideal gas equation.This has 2 effects:

• 1st – the molecules hit the walls slightly less frequently and
• 2nd -they hit with slightly less force and both of these effects make the pressure less than the ideal gas law will predict.

To make up for this the van der Waals equation introduces this term a*(n/V)² , where a = constant for a particular gas.

If molecules are attracted to one another, they don’t fly off as much and hit the walls and this reduces the pressure on the walls of the container. The constant “a” is in fact a measure of the average attraction between molecules. The “a” differs for different substances, after all, not all types of molecules have the same strength of interactions. So, this modification is to take into account the stickiness of the individual molecules.

But why the (n/V)²  term ? -> Well…n/V represents the concentration of a gas. And the more concentrated the gas the closer the molecules are toghether making the attractive forces greater. The term is squared because the attractive forces have 2 effects on the gas molecules. They hit the walls less frequently and with slightly less force. That’s the net effect of the amount of stickiness which is proportional to the density of molecules. This net effect is also proportional to the number of molecules that can interact by this stickiness, which is again proportional to density. And since the density is number divided by volume, the density times density results in a one over volume squared behavior. Therefore the correction term a*(n/V)² corrects the pressure of real gas for the effect of attractive forces between gas molecules.

Looking at VOLUME term in van der Waals equation  expressed as (V-nb), the V represents the measured Volume. Here again, the kinetic theory of ideal gas assumes that the gas molecules themselves have negligible volume. But in a real gas they do in fact occupy some of the volume. And this mean there is slightly less volume available for the molecules to move about it.To make up for this the van der waals equation reduces the measured volume by the factor n*B.Where B is a constant for a particular gas.

But why is the factor of the form n*B? -> ‘b’, is due to the fact that molecules don’t have access to the entire volume of the container. “b” in fact represents the volume that is unavailable because it’s occupied by the gas molecules themselves and this is for 1 mole of the gas, so you multiply it by “n“(the number of the gas in the sample) to get the total volume occupied by the gas molecules.

In order to have more accurate measurement of the real volume occupied by gas molecules we have to subtract off the volume taken up by the molecules themselves. And since the size of molecules differs from substance to substance, this number also depends on the identity of the gas. This correction for Volume term for real gases is necessary because the volume of real gas is much larger than of the ideal gas.

So the van der Waals equation adjusts the measured volume values of P and V for real gases to make them follow the ideal gas law. In reality the ideal gas equation gives pretty accurate results especially at high temperatures of low pressures. So for most purposes it’s good enough to use the ideal gas equation rather  than van der Waals equation.